Function gradient online calculator

The gradient of the function is the vector whose coordinates are partial derivatives of this function with respect to all its variables.

The gradient is denoted by nabla symbol . The gradient expression of some function is written as follows:

where , , - are partial derivatives of the function with respect to variables , , respectively.

The gradient vector points toward the direction of the fastest growth of the function. Consider the graph of the function .

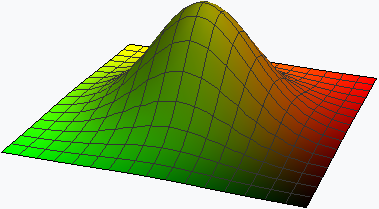
This function reaches its single maximum at the point . The graph of the gradient vector field of the function has the form:

This graph shows, that the gradient vector at each point is directed towards the fastest growth of the function, i.e. to the point . The magnitude of the vector reflects the rate of the function growth at this direction.

The problem of calculating the gradient of the function often arises when searching the extremums of the function using different numerical methods.

Our online calculator is able to find the gradient of almost any function, both in general form and at the specific point, with step by step solution.