Check vectors form the basis online calculator
The basis in -dimensional space is called the ordered system of linearly independent vectors.
For the following description, intoduce some additional concepts.
Expression of the form:
, where − some scalars and is called linear combination of the vectors .
If there are exist the numbers such as at least one of then is not equal to zero (for example ) and the condition:
is hold, the the system of vectors − is called linear-dependent.
If the equality above is hold if and only if, all the numbers , then the system of vectors − is called linear-independent.
The basis can only be formed by the linear-independent system of vectors. The conception of linear dependence/independence of the system of vectors are closely related to the conception of matrix rank.
Our online calculator is able to check whether the system of vectors forms the basis with step by step solution.
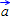 1 by:
1 by: 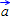 2 by:
2 by: 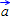 3 by:
3 by: 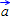 4 by:
4 by:  5 by:
5 by:  6 by:
6 by:  7 by:
7 by:  8 by:
8 by: 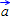 9 by:
9 by: 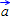 1 = { }
1 = { }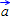 2 = { }
2 = { }See also:
Volume of parallelepiped build on vectors online calculatorVolume of tetrahedron build on vectors online calculator