Разложить вектор по базису онлайн
Любой вектор некоторого -мерного пространства можно представить в виде линейной комбинации базисных векторов этого -мерного пространства и при том единственным образом.
Разложение произвольного -мерного вектора по базису, образованному линейно-независимой системой -мерных векторов выглядит следующим образом:
, где − некоторые числа, являющиеся коэффициентами разложения (линейной комбинации) вектора по базису .
Наш онлайн калькулятор найдет разложение вектора по базису с подробным решением на русском языке.
Разложить вектор по базису
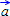 1 по:
1 по: 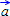 2 по:
2 по: 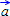 3 по:
3 по: 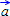 4 по:
4 по: 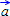 5 по:
5 по: 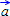 6 по:
6 по: 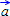 7 по:
7 по: 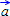 8 по:
8 по:  9 по:
9 по:  по:
по:  1 = { }
1 = { } 2 = { }
2 = { }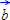 = { }
= { }
Установить калькулятор на свой сайт
Другие полезные разделы:
Смешанное произведение векторов онлайнОбъём параллелепипеда построенного на векторах онлайн