Градиент функции онлайн

Градиент функции - это вектор координатами которого являются частные производные этой функции по всем её переменным.

Градиент обозначается символом набла . Выражение градиента некоторой функции записывается следующим образом:

где , , - частные производные функции по переменным , , соответственно.

Вектор градиента указывает направление наискорейшего роста функции. Рассмотрим график функции .

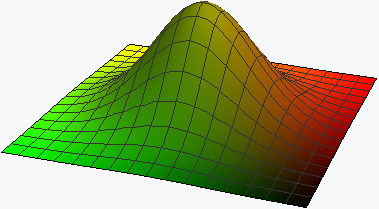
Эта функция достигает своего единственного максимума в точке . График градиентного поля данной функции имеет вид:

Из данного градика видно, что в каждой точке вектор градиента направлен в сторону наискорейшего роста функции, т.е. в точку . При этом модуль вектора отражает скорость роста (крутизну подъёма) функции в этом направлении.

Задача вычисления градиента функции очень часто возникает при поиске эстремумов функции с использованием различных численных методов.

Наш онлайн калькулятор позволяет вычислить градиент практически любой функции как общем виде, так и в конкретной точке с описанием подробного хода решения на русском языке.