Векторное произведение векторов онлайн
Векторное произведение векторов представляет собой вектор, который удовлетворяет следующим условиям:
Величина этого вектора равна произведению модулей (длин) исходных векторов на синус угла между ними:
Этот вектор перпендикулярен каждому из исходных векторов:
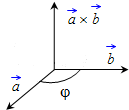
Вектор направлен таким образом, что если смотреть с конца этого вектора, то кратчайший поворот от вектора к вектору осуществляется против часовой стрелки (т.е. тройка векторов является правой).
Векторное произведение обладает следующими свойствами:
Антикоммутативность:
Ассоциативность, относительно числового множителя ():
Дистрибутивность:
Векторное произведение векторов вычисляется по формуле:
Наш онлайн калькулятор находит векторное произведение векторов с описанием подробного хода решения на русском языке.
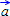 по:
по: 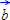 по:
по: 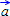 = { }
= { }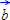 = { }
= { }Другие полезные разделы:
Решение неравенств онлайнКалькулятор сходимости рядов
Скалярное произведение векторов онлайн
Смешанное произведение векторов онлайн